Answer:
Part a)

Part b)
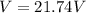
Part c)
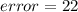 %
%
Step-by-step explanation:
Part a)
When voltmeter of 10 k ohm is used to measure the voltage across the given resistor then we will have
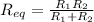
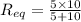
 ohm
ohm
now the current through the given cell is

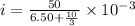

now voltage across 5 k ohm resistor is given as

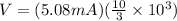

Part b)
If there is not voltmeter connected across 5 k ohm
then current in the circuit is given as
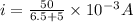

Now voltage across 5 k ohm resistor
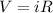
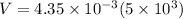
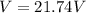
Part c)
percentage error in the reading is given as
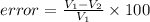
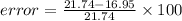
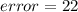 %
%