Question

Show the processes for solving 2x+3y=5 and 4x - y=17 using elimination and substitution

Answer 1

The solution of the two equations 2x+3y=5 and 4x - y=17 is (4, -1).

SOLUTION:

Given, two linear equations are 2x + 3y = 5 → (1) and 4x – y = 17 → (2).

Let us first solve the above equations using elimination process.

For elimination, one of the coefficients of variables has to be same in order to cancel them.

Now solve (1) and (2)

eqn (1)
`*` 2 → 4x + 6y = 10

eqn (2) → 4x – y = 17

(-) ----------------------------

0x + 7y = -7

y = -1

Substitute y value in (2)

`4 x-(-1)=17 \rightarrow 4 x+1=17 \rightarrow 4 x=17-1 \rightarrow 4 x=16 \rightarrow x=4`

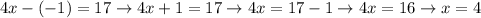
So, solution of two equations is (4, -1).

Now let us solve using substitution process.

Then, (2) → 4x – y = 17 → 4x = 17 + y → y = 4x – 17

Now substitute y value in (1) → 2x + 3(4x – 17) = 5 → 2x + 12x – 51 = 5 → 14x = 5 + 51 → 14x = 56

x = 4

Substitute x value in (2) → y = 4(4) – 17 → y = 16 – 17 → y = -1

Hence, the solution of the two equations is (4, -1).