Question

Suppose a chef claims that her meatball weight is less than 4 ounces, on average. Several of her customers do not believe her, so the chef decides to do a hypothesis test, at a 10% significance level, to persuade them. She cooks 14 meatballs. The mean weight of the sample meatballs is 3.7 ounces. The chef knows from experience that the standard deviation for her meatball weight is 0.5 ounces. H0: μ=4; Ha: μ<4 α=0.1 (significance level) What is the test statistic (z-score) of this one-mean hypothesis test, rounded to two decimal places? Provide your answer below:

Answer 1

The value of test static we get is - 2.24

As per given information,

Sample n = 14

Mean X 3.7

Standard deviation = σ = 0.5

Null and alternative hypotheses:

Ηο: μ > 4

Ha : μ < 4

From these we can say that it is a left-tailed test.

The test static is

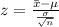
`z =(\bar x-\mu)/((\sigma)/(√(n) ) )`

z =
`(3.7-4)/((0.5)/(√(14) ) )`

z =
`(-0.3)/(0.13363)`

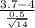
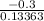
z = - 2.244994431

After rounding off the value of z is - 2.24

Answer 2

z = -2.24

Explanation:

The test statistic for testing a claim about a mean (when we know the standard deviation of the population) is:

`z=(x-u)/((s)/(√(n) ) )`

where z is the test statistic, x is the sample mean, u is the population mean, s is the standard deviation of the population and n is the number of meatballs in this case.

`z=(3.7-4)/((0.5)/(√(14) ) )=-2.24`