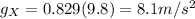Question

If the mass of a planet is 0.231 mE and its radius is 0.528 rE, estimate the gravitational field g at the surface of the planet. The gravitational acceleration on Earth is 9.8 m/s 2 and the value of the universal gravitational constant is 6.67259 × 10−11 N · m2 /kg2 . Answer in units of m/s 2 .

Answer 1

`8.1 m/s^2`

Step-by-step explanation:

The strength of the gravitational field at the surface of a planet is given by

`g=(GM)/(R^2)` (1)

where

G is the gravitational constant

M is the mass of the planet

R is the radius of the planet

For the Earth:

`g_E = (GM_E)/(R_E^2)=9.8 m/s^2`

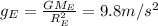
For the unknown planet,

`M_X = 0.231 M_E\\R_X = 0.528 R_E`

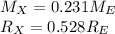
Substituting into the eq.(1), we find the gravitational acceleration of planet X relative to that of the Earth:

`g_X = (GM_X)/(R_X^2)=(G(0.231M_E))/((0.528R_E)^2)=(0.231)/(0.528^2)((GM_E)/(R_E^2))=0.829 g_E`

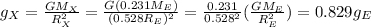
And substituting g = 9.8 m/s^2,

`g_X = 0.829(9.8)=8.1 m/s^2`