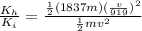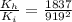Answer:

Step-by-step explanation:
As we know that there is no external force on the system of hydrogen atom and electron so we will say momentum is conserved
so we will have
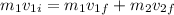
here we know that
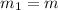
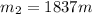
now we have
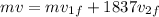

also we know that
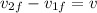
now we will have
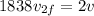
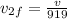
now we need to find the ratio of kinetic energy of hydrogen atom with initial kinetic energy
so it is given as