Answer:
a) The probability that a student has either a Visa card or a MasterCard is 0.71.
b) V and M are not independent.
Step-by-step explanation:
Given : The probability that a student has a Visa card (event V) is 0.63. The probability that a student has a MasterCard (event M) is 0.11. The probability that a student has both cards is 0.03.
To find :
a) The probability that a student has either a Visa card or a MasterCard ?
b) In this problem, are V and M independent ?
Solution :
The probability that a student has a visa card(event V) is P(V)= 0.63
The probability that a student has a MasterCard (event M) is P(M)= 0.11
The probability that a student has both cards is
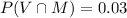
a) Probability that a student has either a Visa card or a Master Card is given by,
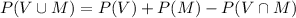


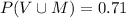
The probability that a student has either a Visa card or a MasterCard is 0.71.
b) Two events, A and B, are independent if
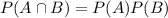
For V and M to be independent the condition is satisfied,
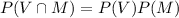
Substitute the values,
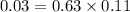
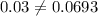
So, V and M are not independent.