Question

The mileage of a new model SUV on the interstate highway has been stated by the manufacturer as having a mean of 20 mpg and a standard deviation of 3.0 mpg. A consumer agency intends to sample 36 cars and test them. Find the probability that the sample average will be over 21.0 mpg. (Assume that mileage is normally distributed.)

Answer 1

Answer: 0.0227502

Explanation:

Let x denote the random variable that represents the mileage of SUV.

As per given we have,

`\mu = 20`

`\sigma = 3`

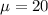
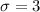
sample size : n= 36

We assume that the mileage of SUV is normally distributed.

Z-score value corresponds to x= 21.0,

`z=(x-\mu)/((\sigma)/(√(n)))=\frac{21-20}{\frac{3}{\frac{}{36}}}=2`

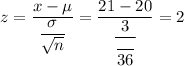
Using standard z-value table ,

The probability that the sample average will be over 21.0 mpg:-

P(X>35)=P(z>2)=1-P(z<2)=1-0.9772498=0.0227502

Hence, the required probability = 0.0227502