Answer and explanation:
Given : Consider the Ideal Gas Law,
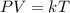 where k>0 is a constant.
where k>0 is a constant.
To find : Solve this equation for V in terms of P and T.
Solution :
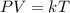
Divide each side by P,
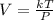 ....(1)
....(1)
a) Determine the rate of change of the volume with respect to the pressure at constant temperature. Interpret the result.
Differentiate equation (1) w.r.t P,
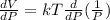
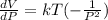
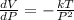
b) Determine the rate of change of the volume with respect to the temperature at constant pressure. Interpret the result.
Differentiate equation (1) w.r.t T,
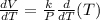
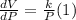
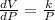
c) Assuming k =1, draw several level curves of the volume function and interpret the results.
When k=1,
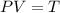
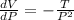 <0
<0
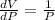 >0
>0
Refer the attached figure below.