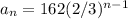Question

Find the common ratio and an explicit form in each of the following geometric sequences.

b. 162, 108, 72, 48, ...

Answer 1

The explicit form is
`a_(n)=162(2/3)^(n-1)`

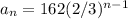
Explanation:

The explicit form of a geometric sequence is given by:

`a_(n)=ar^(n-1)`

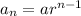
where an is the nth term, a is the first term of the sequence and r is the common ratio.

In this case:

a=162

The value of the common ratio is obtained by dividing one term by the previous term.

For the first and second terms:

108/162=2/3

For the second and third terms (In order to prove that 2/3 is the common ratio)

72/108=2/3

Therefore:

r=2/3

Replacing a and r in the formula:

`a_(n)=162(2/3)^(n-1)`