Question

The probability that the noise level of a wide-band amplifier will exceed 2 dB is 0.05 independently of every other amplifier. Consider a concert hall with 12 such amplifiers. b) Find the probability that at most two will exceed 2dB. Please set up your equations in your work. Also please round your answer to the nearest three decimal places.

Answer 1

0.980

Explanation:

The probability that the noise level of a wide-band amplifier will exceed 2 dB is 0.05

So, probability of success = 0.05

Probability of failure = 1-0.05=0.95

There are 12 amplifiers

We are supposed to find the probability that at most two will exceed 2dB.

We will use binomial distribution

Formula :
`P(X=r)=^nC_r p^r q ^(n-r)`

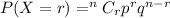
p = 0.05

q = 0.95

n = 12

We are supposed to find the probability that at most two will exceed 2dB.

So,
`P(X\leq 2)=P(X=0)+P(X=1)+P(X=2)`

`P(X\leq 2)=^(12)C_0 P(0.05)^0 (0.95)^(12-0)+^(12)C_1 P(0.05)^1(0.95)^(12-1)+^(12)C_2 P(0.05)^2 (0.95)^(12-2)`

`P(X\leq 2)=(12!)/(0!(12-0)!) (0.05)^0 (0.95)^(12-0)+(12!)/(1!(12-1)!)(0.05)^1(0.95)^(12-1)+(12!)/(2!(12-2)!) (0.05)^2 (0.95)^(12-2)`

`P(X\leq 2)=0.980`

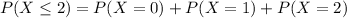
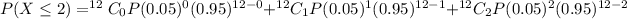
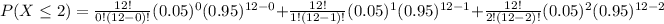
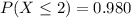
Hence the probability that at most two will exceed 2dB is 0.980