Solve 2x^2 + x - 4 = 0

Question

asked May 12, 2020 210k views

2 Answers

Mychelle · Answer 1 · 2020-05-18T01:10:39+0000

The solution of 2x^2 + x - 4 = 0 is x = 1.186 or -1.686

Solution:

A two degree polynomial equation is given in the question.

We have been asked to solve it to find the value of ‘x’.

The given equation is
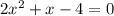
2 x^(2)+x-4=0

There are two ways to solve this equation.

We can either factorise it or use the quadratic equation formula. For factorising it, it has to satisfy certain conditions.

The condition is
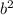b^2 - 4ac should be a perfect square otherwise the equation is not factorable.

a = 2, b = 1, c = -4

On substituting the values, we get;

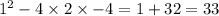
1^(2)-4 * 2 *-4=1+32=33

Which is not a perfect square.

Hence we have to use the quadratic equation is

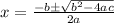
$x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}$

By substituting the values of a,b and in the quadratic equations. We get;

$\begin{array}{l}{x=\frac{-1 \pm \sqrt{1^(2)-4 * 2 *-4}}{2 * 2}} \\\\ {x=(-1 \pm √(33))/(2 * 2)}\end{array}$

The two roots of x are:

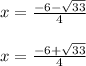
$\begin{array}{l}{x=(-6-√(33))/(4)} \\\\ {x=(-6+√(33))/(4)}\end{array}$

On solving both the equations we will get the roots of the given equation, which are:

x = 1.186 or -1.686