Answer: The electron moves
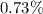 less fast than light
less fast than light
Step-by-step explanation:
The complete question is written below:
The mass of an electron is
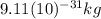 . If the de Broglie wavelength for an electron in a hydrogen atom is
. If the de Broglie wavelength for an electron in a hydrogen atom is
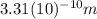 , how fast is the electron moving relative to the speed of light? The speed of light is
, how fast is the electron moving relative to the speed of light? The speed of light is
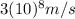 .
.
The De Broglie wavelength equation is:
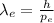 (1)
(1)
Where:
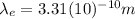 is the de broglie wavelength for an electron
is the de broglie wavelength for an electron
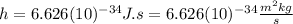 is the Planck constant
is the Planck constant
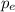 is the momentum of the electron
is the momentum of the electron
On the other hand, the momentum of the electron is given by:
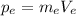 (2)
(2)
Where:
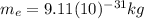 is the mass of the electron
is the mass of the electron
 is the velocity of the electron
is the velocity of the electron
Substituting (2) in (1):
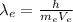 (3)
(3)
Isolating
 :
:
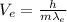 (4)
(4)
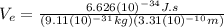
Finally:
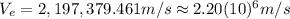 This is the velocity of the electron
This is the velocity of the electron
Calculating the ratio between the velocity of the electron and the velocity of a photon:
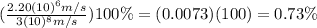
Therefore, the electron moves
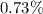 less fast than the photon (light).
less fast than the photon (light).