Question

(a)- If F(x) = f(x)g(x), where f and g have derivatives of all orders, show that F"=f''g+2f'g'+fg'' (b)- Find simmiliar formula for F''' and F^(4) (c)-Describe the pattern for higher derivatives of F.

Answer 1

See proof below

Explanation:

By the rule of the derivative of a product and sum (we will omit the argument x to make clearer the calculations)

F' = (fg)' = f'g + fg'

F'' = (f'g + fg')' = (f'g)' + (fg')' = (f''g+f'g') + (f'g'+fg'') =

f''g + 2f'g' + fg''

b) In a similar way, we can find that

F''' and
`\bf F^((4))` are

F''' = f'''g + 3f''g' + 3 f'g'' + fg'''

`\bf F^((4)) = f^((4))g+4f'''g'+6f''g''+4f'g'''+fg^((4))`

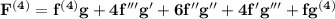
c)

The pattern for higher derivatives resemble the Newton's binomial:

`\bf F{(n)}=\binom{n}{0}f^((n))g^((0))+\binom{n}{1}f^((n-1))g^((1))+\binom{n}{2}f^((n-2))g^((2))+...+\binom{n}{n}f^((0))g^((n))`

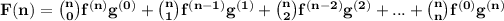
where

`\bf f^((0))` means no derivative and

`\bf \binom{n}{m}` are the combination of n elements taken m at a time

`\bf \binom{n}{m}=(n!)/(m!(n-m)!)`