Question

Use the properties of logarithms to rewrite each expression in an equivalent form containing a single logarithm.

1/2 log(16) + log(3) + log 1/4

Answer 1

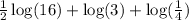`(1)/(2)\log(16) + \log(3) + \log((1)/(4))` = log(3)

Explanation:

Given equation:

`(1)/(2)\log(16) + \log(3) + \log((1)/(4))`

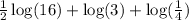
now,

we know the properties of log function as:

1) log(A) + log(B) = log(AB)

2) log(A) - log(B) =
`\log((A)/(B))`

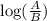
3) log(Aᵇ) = b × log(A)

therefore,

using property 3 we get

`\log(16)^{(1)/(2)} + \log(3) + \log((1)/(4))`

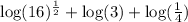
or

`\log(4) + \log(3) + \log((1)/(4))`

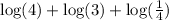
now,

using the property 2 we get

⇒ log(4) + log(3) + log(1) - log(4)

or

⇒ log(3) + log(1)

now,

using the property 1, we get

⇒ log(3 × 1)

or

⇒ log(3)