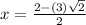Answer:
x = 3 + √6 ; x = 3 - √6 ;
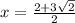 ;
;
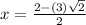
Explanation:
Relation given in the question:
(x² − 6x +3)(2x² − 4x − 7) = 0
Now,
for the above relation to be true the following condition must be followed:
Either (x² − 6x +3) = 0 ............(1)
or
(2x² − 4x − 7) = 0 ..........(2)
now considering the equation (1)
(x² − 6x +3) = 0
the roots can be found out as:
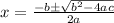
for the equation ax² + bx + c = 0
thus,
the roots are
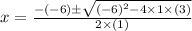
or
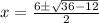
or
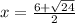 and, x =
and, x =
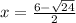
or
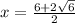 and, x =
and, x =
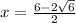
or
x = 3 + √6 and x = 3 - √6
similarly for (2x² − 4x − 7) = 0.
we have
the roots are
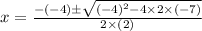
or
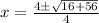
or
 and, x =
and, x =
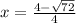
or
 and, x =
and, x =
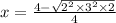
or
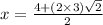 and, x =
and, x =

or
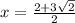 and,
and,
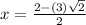
Hence, the possible roots are
x = 3 + √6 ; x = 3 - √6 ;
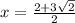 ;
;