Question

In an article about the cost of health care, USA Today reported that a visit to a hospital emergency room has a mean cost of $1400 in 2017. Assume that the cost for the hospital emergency room visit is normally distributed with a standard deviation of $392. Answer the following questions about the cost of a hospital emergency room visit for this medical service. What is the probability that the cost will be more than $1000?

Answer 1

Answer: 0.8461

Explanation:

Given :
`\mu=144\ \ ; \sigma=392`

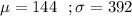
Let x be the random variable that represents the cost for the hospital emergency room visit.

We assume that cost for the hospital emergency room visit is normally distributed .

z-score for x=1000 ,

`z=(1000-1400)/(392)\approx-1.02\ \ \ [\because z=(x-\mu)/(\sigma)]`

Using z-value table , we have

P-value =P(x>1000)=P(z>-1.02)=1-P(z≤ -1.02)=1-0.1538642

=0.8461358≈0.8461 [Rounded nearest 4 decimal places]

Hence, the probability that the cost will be more than $1000 = 0.8461