Question

Use 90°<θ<180° and sin θ=24/25 ⁡to answer the following questions. What is cos⁡ θ?

Answer 1

-7/25

Explanation:

`\theta` is in quadrant two given that
`\theta` is between 90 degrees and 180 degrees.

This means cosine value there is negative and sine value is positive.

Let's use the Pythagorean Identity:
`\sin^2(\theta)+\cos^2(\theta)=1`.

`((24)/(25))^2+\cos^2(\theta)=1`

`(576)/(625)+\cos^2(\theta)=1`

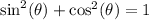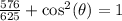
Subtract 576/625 on both sides:

`\cos^2(\theta)=1-(576)/(625)`

`\cos^2(\theta)=(625-576)/(625)`

`\cos^2(\theta)=(49)/(625)`

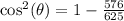
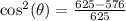
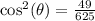
Take the square root of both sides:

`\cos(\theta)=\pm (7)/(25)`

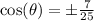
So recall that the cosine value here is negative due to the quadrant we are in.

`\cos(\theta)=-(7)/(25)`

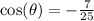
Check:

`((24)/(25))^2+(-(7)/(25))^2`

`(576+49)/(625)`

`(625)/(625)`

`1`

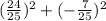
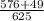
So we got the desired result since the right hand side of our Pythagorean Identity is 1.