Question

Assume that there are 14 board members: 9 females, and 5 males including Mark. There are 3 tasks to be assigned. Note that assigning the same people different tasks constitutes a different assignment.

1) Find the probability that both males and females are given a task.

2) Find the probability that Mark and at least one female are given tasks.

Answer 1

Total members = 14

Total tasks = 3

So, total outcomes =
`^(14)C_3`

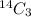
1) Find the probability that both males and females are given a task.

No. of females = 9

No. of males = 5

Favorable events = 2 female 1 male + 2 male 1 male =
`9C_2 * 5C_1 +9C_1 * 5C_2`

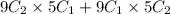
So, the probability that both males and females are given a task:

=
`(^9C_2 * ^5C_1 +9C_1 * ^5C_2)/(^(14)C_3)`

=
`((9!)/(2!(9-2)!) * (5!)/(1!(5-1)!) +(9!)/(1!(9-1)!) * (5!)/(2!(5-2)!))/((14!)/(3!(14-3)!))`

=
`0.7417`

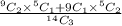
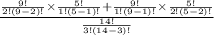
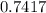
So, the probability that both males and females are given a task is 0.7417

2)Find the probability that Mark and at least one female are given tasks.

Since mark is fixed , so places are left

So, favorable events = 2 female + 1 female 1 male =
`^9C_2 +^4C_1 * ^9C_1`

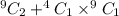
So, the probability that Mark and at least one female are given tasks. :

=
`(^9C_2 +^4C_1 * ^9C_1)/(^(13)C_2)`

=
`((9!)/(2!(9-2)!) +(4!)/(1!(4-1)!) * (9!)/(1!(9-1)!) )/((13!)/(2!(13-2)!))`

=
`0.9230`

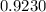
So, The probability that Mark and at least one female are given tasks is 0.9230