Answer:
There is a significant difference between the two means based on this samples at the 0.10 level of significance.
Explanation:
Let's call
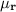 mean of the systolic pressure from the right hand
mean of the systolic pressure from the right hand
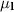 mean of the systolic pressure from the left hand
mean of the systolic pressure from the left hand
and construct a confidence interval for the difference
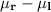
based on the sample of size 5.
The confidence interval whose endpoints are
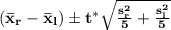
where
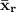 = mean of the sample from the right hand
= mean of the sample from the right hand
 = mean of the sample from the left hand
= mean of the sample from the left hand
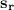 = standard deviation of the sample from the right hand
= standard deviation of the sample from the right hand
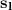 = standard deviation of the sample from the left hand
= standard deviation of the sample from the left hand
 = t-score corresponding to a level of significance 0.10 or a confidence level 90%
= t-score corresponding to a level of significance 0.10 or a confidence level 90%
Since the sample is too small we have better use the Student's t-distribution with 4 (sample size -1) degrees of freedom, which is the approximation of the Normal distribution for small samples.
For a 90% confidence level
 equals 2.132
equals 2.132
Let's compute now the means and standard deviations of the samples
From the right hand we have
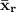 = 139.2
= 139.2
 = 7.66
= 7.66
From the left hand we have
 = 164.6
= 164.6
 = 16.85
= 16.85
Then our confidence interval would be
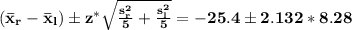
finally, the interval is
[-43.05, -7.75]
Since our confidence interval does not contain the zero, we can say there is a significant difference between the two means based on this samples at the 0.10 level of significance.