Question

The chamber of commerce of a Florida Gulf Coast community advertises that area residential property is available at a mean cost of $125,000 or less per lot. Suppose a sample of 32 properties provided a sample mean of $130,000 per lot and a sample standard deviation of $12,500. Use a .05 level of significance to test the validity of the advertising claim.

Answer 1

Answer: Reject the null hypothesis.

Step-by-step explanation: As per given , we have

`H_0: \mu\leq125000`

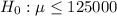
`H_a: \mu>125000` ,Since
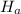`H_a` is right=-tailed , so the test is right -tailed test.

Sample size : n= 32 > 30 , so we use z-test.

`\overline{x}=130,000`

`s=12,500`

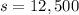
Test statistic :
`z=\frac{\overline{x}-\mu}{(s)/(√(n))}`

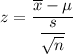
i.e.
`z=(130000-125000)/((12500)/(√(32)))`

`=2.2627416998\approx2.26`

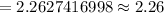
Using standard z-value table for right tailed test , we have

P-value=
`P(z>2.26)=0.0119106`

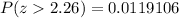
Since , the p-value (0.0119106) is less than significance level , so we reject the null hypothesis.

We conclude that there is sufficient evidence to reject the advertising claim.