Answer:
The total number of ways are 264,264
Explanation:
Consider the provided information.
The Mathletes Club has 15 members and is electing a 5-member committee.
One of the members, Alice, has set a condition that, if she is not elected president, then she will not accept any position in the committee.
Case I: If she is elected as president.
If she is elected as president so now we have 14 members and is electing a 4-member committee. (vice-president, secretary, treasurer, and sergeant-at-arms).
No ways:

Case II: If she is not elected as president.
If she is not elected as president so now we have 14 members and is electing a 5-member committee. (president, vice-president, secretary, treasurer, and sergeant-at-arms)
No ways:
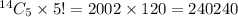
Hence, the total number of ways are:
24,024+240,240=264,264
Hence, the total number of ways are 264,264