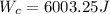Question

A cave rescue team lifts an injured spelunker directly upward and out of a sinkhole by means of a motor-driven cable. The lift is performed in three stages, each requiring a vertical distance of 11.0 m: (a) the initially stationary spelunker is accelerated to a speed of 1.10 m/s; (b) he is then lifted at the constant speed of 1.10 m/s; (c) finally he is decelerated to zero speed. How much work is done on the 78.0 kg rescue by the force lifting him during each stage?

Answer 1

Mass m = 78 kg

Vertical height in each stage h = 11 m

(a).

Initial speed u = 0

Final speed v = 1.1 m / s

`v^2=u^2 + 2 as`

`1.1^2 = 2 a * 11`

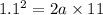
a = 0.055 m/s²

Work done

`W_a= m g h + (1)/(2)mv^2`

`W_a= 78* 9.8 * 11 + (1)/(2) 78 * 1.1^2`

`W_a = 8408.4 + 47.19`

`W_a = 8455.59 J`

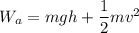
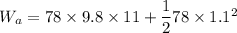
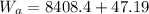
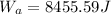
(b).Work done

`W_b= mgh`

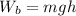
W_b = 78× 9.8× 11

`W_b= 8408.4 J`

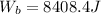
c)

Work done

`W= m g h + (1)/(2)m(v_f-v_i)^2`

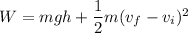
Where V = final speed

= 0

v = 1.1 m / s

for deceleration a = -0.055 m/s²

now,

`F_L = 56 (-0.055+9.8) = 545.72 N`

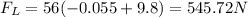
W_c = 545.75 × 11

`W_c = 6003.25 J`