Question

The World Health Organization's (W.H.O.) recommended daily minimum of calories is 2600 per individual. The average number of calories ingested per capita per day for the US is approximately 2460 with a standard deviation of 500. If we take a random sample of 36 individuals from the US, what is the probability that the sample mean exceeds the W.H.O. minimum?

Answer 1

The probability is 0.046

Solution:

As per the question:

Minimum calorie intake of an individual per day,
`bar{X} = 2600`

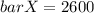
The no. of calories ingestion on an average per day per capita, Mean
`(\mu) = 2460`

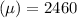
Standard deviation,
`\sigma = 500`

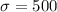
No. of individuals in a random sample, n = 36

Now,

The Probability for the sample mean to exceed the WHO minimum is given by:

P(
`\bar{X} geq 2600) = [tex]\frac{\bar{X} - \mu}{(\sigma)/(n)}`

P(
`\bar{X} geq 2600) = [tex](2600 - 2460)/((500)/(6)) = 1.68`

Now, with the help of Standard Normal table:

P(Z > 1.68) = 0.0046