Answer: Satellite X has a greater period and a slower tangential speed than Satellite Y
Step-by-step explanation:
According to Kepler’s Third Law of Planetary motion “The square of the orbital period of a planet is proportional to the cube of the semi-major axis (size) of its orbit”.
 (1)
(1)
Where;
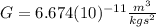 is the Gravitational Constant
is the Gravitational Constant
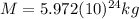 is the mass of the Earth
is the mass of the Earth
 is the semimajor axis of the orbit each satellite describes around Earth (assuming it is a circular orbit, the semimajor axis is equal to the radius of the orbit)
is the semimajor axis of the orbit each satellite describes around Earth (assuming it is a circular orbit, the semimajor axis is equal to the radius of the orbit)
So for satellite X, the orbital period
 is:
is:
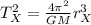 (2)
(2)
Where
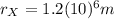
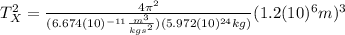 (3)
(3)
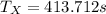 (4)
(4)
For satellite Y, the orbital period
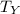 is:
is:
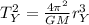 (5)
(5)
Where
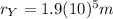
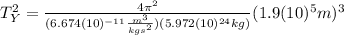 (6)
(6)
 (7)
(7)
This means

Now let's calculate the tangential speed for both satellites:
For Satellite X:
 (8)
(8)

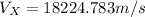 (9)
(9)
For Satellite Y:
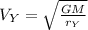 (10)
(10)
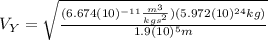
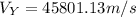 (11)
(11)
This means
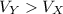
Therefore:
Satellite X has a greater period and a slower tangential speed than Satellite Y