Question

Two competitive neighbours build rectangular pools that cover the same area but are different shapes. Pool A has a width of (x + 3)m and a length that is 3m longer than its width. Pool B has a length that is double the width of Pool A. The width of Pool B is 4m shorter than its length.

a. Find the exact dimensions of each pool if their areas are the same.
b. Verify that the areas are the same.

Answer 1

a)Dimensions of pool A are length = 6.667m and width = 3.667 m and dimension of pool B are length = 7.333m and width = 3.333m.

b) Area of pool A is equal to area of pool B equal to 24.44 meters.

Solution:

Let’s first calculate area of pool A .

Given that width of the pool A = (x+3)

Length of the pool A is 3 meter longer than its width.

So length of pool A = (x+3) + 3 =(x + 6)

Area of rectangle = length x width

So area of pool A =(x+6) (x+3) ------(1)

Let’s calculate area of pool B

Given that length of pool B is double of width of pool A.

So length of pool B = 2(x+3) =(2x + 6) m

Width of pool B is 4 meter shorter than its length,

So width of pool B = (2x +6 ) – 4 = 2x + 2

Area of rectangle = length x width

So area of pool B =(2x+6)(2x+2) ------(2)

Since area of pool A is equal to area of pool B, so from equation (1) and (2)

(x+6) (x+3) =(2x+6) (2x+2)

On solving above equation for x

(x+6) (x+3) =2(x+3) (2x+2)

x+6 = 4x + 4

x-4x = 4 – 6

x =
`(2)/(3)`

Dimension of pool A

Length = x+6 = (
`(2)/(3)`) +6 = 6.667m

Width = x +3 = (
`(2)/(3)`) +3 = 3.667m

Dimension of pool B

Length = 2x +6 = 2(
`(2)/(3)`) + 6 =
`(22)/(3)` = 7.333m

Width = 2x + 2 = 2(
`(2)/(3)`) + 2 =
`(10)/(3)` = 3.333m

Verifying the area:

Area of pool A = (
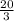`(20)/(3)`) x (
`(11)/(3)`) =
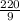`(220)/(9)` = 24.44 meter

Area of pool B = (
`(22)/(3)`) x (
`(10)/(3)`) =
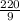`(220)/(9)` = 24.44 meter

Summarizing the results:

(a)Dimensions of pool A are length = 6.667m and width = 3.667 m and dimension of pool B are length = 7.333m and width = 3.333m.

(b)Area of pool A is equal to Area of pool B equal to 24.44 meters.