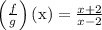Answer:
The arithmetic combinations of given functions are (f + g)(x) = 2x, (f - g)(x) = 4, (f
 g)(x) =
g)(x) =
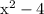 ,
,
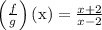
Solution:
Given, two functions are f(x) = x + 2 and g(x) = x – 2
We need to find the arithmetic combinations of given two functions .
Arithmetic functions of f(x) and g(x) are (f + g)(x), (f – g)(x), (f
 g)(x),
g)(x),

Now, (f + g)(x) = f(x) + g(x)
= x + 2 +x – 2
= 2x
Therefore (f + g)(x) = 2x
similarly,
(f - g)(x) = f(x) - g(x)
= x + 2 –(x – 2)
= x + 2 –x + 2
= 4
Therefore (f - g)(x) = 4
similarly,
(f
 g)(x) = f(x)
g)(x) = f(x)
 g(x)
g(x)
= (x + 2)
 (x – 2)
(x – 2)
= x
 (x – 2) + 2
(x – 2) + 2
 (x -2)
(x -2)

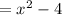
Therefore (f
 g)(x) =
g)(x) =
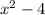
now,
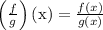
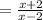
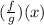 =
=
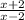
Hence arithmetic combinations of given functions are (f + g)(x) = 2x, (f - g)(x) = 4, (f
 g)(x) =
g)(x) =
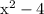 ,
,