Question

A manufacturer produces a large number of toasters. From past experience, the manufacturer knows that approximately 1% are defective. In a quality control procedure, we randomly select 50 toasters for testing. We want to determine the probability that no more than one of these toasters is defective.

Answer 1

The probability is 0.9106

Explanation:

The variable that says the number of defective toasters follows a binomial distribution, where we have n identical and independent events (50 toasters) with a probability p of success (1% are defective) and a probability 1-p of fail (99% are not defective). So the probability that x toasters from the 50 are defective is:

`P(x) = (n!)/(x!(n-x)!)*p^(x)*(1-p)^(n-x) \\P(x) = (50!)/(x!(50-x)!)*0.01^(x)*(1-0.01)^(50-x)`

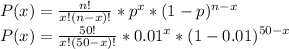
Then, the probability P that no more than one of these toasters is defective is:

P = P(0) + P(1)

So, P(0) and P(1) are calculated as:

`P(0)=(50!)/(0!(50-0)!)*0.01^(0)*(1-0.01)^(50-0)=0.6050`

`P(1)=(50!)/(1!(50-1)!)*0.01^(1)*(1-0.01)^(50-1)=0.3056`

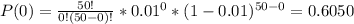
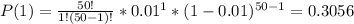
Finally, P is equal to:

P = 0.6050 + 0.3056 = 0.9106