Question

For a recent season in college football, the total number of rushing yards for that season is recorded for each running back. The mean number of rushing yards for the running backs that season is 790 yards. One running back had 1,637 rushing yards for the season, which is 2.42 standard deviations above the mean number of rushing yards. What is the standard deviation of the number of rushing yards for the running backs that season?

Answer 1

The standard deviation of the number of rushing yards for the running backs that season is 350.

Explanation:

Consider the provided information.

The mean number of rushing yards for the running backs that season is 790 yards. One running back had 1,637 rushing yards for the season, which is 2.42 standard deviations above the mean number of rushing yards.

Here it is given that mean is 790 and 1637 is 2.42 standard deviations above the mean.

Use the formula:
`z=(x-\mu)/(\sigma)`

Here z is 2.42 and μ is 790, substitute the respective values as shown.

`2.42=(1637-790)/(\sigma)`

`\sigma=(847)/(2.42)`

`\sigma=350`

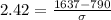
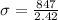
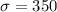
Hence, the standard deviation of the number of rushing yards for the running backs that season is 350.