Question

Find the equivalent thickness of CO2 on Earth.

Earth’s atmospheric CO2 = 3.2 × 1015 kg

Earth’s radius = 6.4 × 106 m

Molar volume (@STP) = 22.414 L mol-1

Answer 1

h = 9483 m

Step-by-step explanation:

Assume Re as radius of earth and h as equivalent thickness of co_2

total volume occupied by
`co_2 = (4)/(3) \pi Re^3 +(4)/(3) \pi (Re+ h)^3`

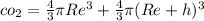
mass of
`co_2 = 3.2 * 10^(15) kg`

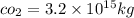
1 mole of co_2 has 44 g mass

1 g has = 1/44 mole

`3.2 * 10^(15) kg  has = 1/44 * 3.2* 10^(18) = 7.27 * 10^(16) mole`

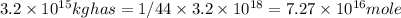
total volume by
`co_2 =  7.27 * 10^(16) * 22.414 L = 163.01* 10^(16) L`

`163.01* 10^(16) L = frac{4}{3} \pi Re^3 +(4)/(3) \pi (Re+ h)^3`

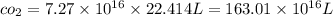
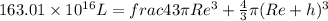
SOLVING RIGHT SIDE WE GET

`h ( Re^2 +h^2 + Reh)  = (3* 163.01* 10^(16))/(4\pi)`

`h ( Re^2 +h^2 + Reh)  =  (3* 163.01* 10^(16))/(4\pi)`

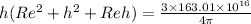
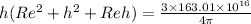
solving for h we get

h = 9483 m