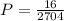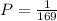Answer:
a)
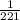
b)

Explanation:
Given : Suppose that two cards are randomly selected from a standard 52-card deck.
We know, In set of 52 -cards deck two sets of 26 are back and red and further into four of 13 sets spade,club,diamond,heart with numbers (2,3,4,5,6,7,8,9,10,J,Q,K,Q,A)
(a) What is the probability that the first card is a king and the second card is a king if the sampling is done without replacement?
Number of kings = 4
Probability of getting first card is a king
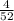
The second card is a king if the sampling is done without replacement
Probability of getting second card is a king

The probability that the first card is a king and the second card is a king if the sampling is done without replacement is given by,
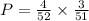
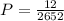
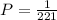
(b) What is the probability that the first card is a king and the second card is a king if the sampling is done with replacement?
Number of kings = 4
Probability of getting first card is a king
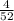
The second card is a king if the sampling is done with replacement
Probability of getting second card is a king
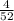
The probability that the first card is a king and the second card is a king if the sampling is done with replacement is given by,