Question

Marketing Docs prepares marketing plans for growing businesses. For 2017, budgeted revenues are $1,500,000 based on 500 marketing plans at an average rate per plan of $3,000. The company would like to achieve a margin of safety percentage of at least 45%. The company’s current fixed costs are $400,000 and variable costs average $2,000 per marketing plan. (Consider each of the following separately.) Required Calculate Marketing Docs’ breakeven point and margin of safety in units. Which of the following changes would help Marketing Docs achieve its desired margin of safety? The average revenue per customer increases to $4,000. The planned number of marketing plans prepared increases by 5%. Marketing Docs purchases new software that results in a 5% increase to fixed costs but reduces variable costs by 10% per marketing plan.

Answer 1

Option (a) is correct.

Step-by-step explanation:

Contribution margin per marketing plan = Sales - Variable cost

= $3,000 - $2,000

= $1,000

A.

(1)
`Break-even\ in\ rooms=(Fixed\ cost)/(contribution\ margin\ per\ marketing\ plan)`

`Break-even\ in\ rooms=(400,000)/(1,000)`

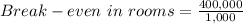
Break even in marketing plan = 400

(2) Break-even in dollars:

= Break-even in marketing plan × Average rate per plan

= 400 × 3,000

= 1,200,000

(3) Margin of safety = Actual sales - Break-even sales in dollars

= 1,500,000 - 1,200,000

= 300,000

`Margin\ of\ safety\ ratio=(Margin\ of\ safety)/(Actual\ sales)`

`Margin\ of\ safety\ ratio=(300,000)/(1,500,000)`

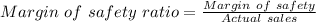
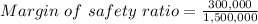
= 20%

B.

(1) Contribution margin per marketing plan = Sales - Variable cost

= $4,000 - $2,000

= $2,000

`Break-even\ in\ rooms=(Fixed\ cost)/(contribution\ margin\ per\ marketing\ plan)`

`Break-even\ in\ rooms=(400,000)/(2,000)`

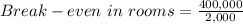
Break even in marketing plan = 200

(2) Break-even in dollars:

= Break-even in marketing plan × Average rate per plan

= 200 × 4,000

= 800,000

(3) Margin of safety = Actual sales - Break-even sales in dollars

= 1,500,000 - 800,000

= 700,000

`Margin\ of\ safety\ ratio=(Margin\ of\ safety)/(Actual\ sales)`

`Margin\ of\ safety\ ratio=(700,000)/(1,500,000)`

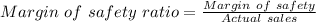
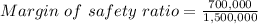
= 47%

Therefore, option (a) would achieve the margin of safety ratio more than 45%.