Question

Twenty percent of all telephones of a certain type are submitted for service while under warranty. Of these, 60% can be repaired, whereas the other 40% must be replaced with new units. If a company purchases ten of these telephones, what is the probability that exactly three will end up being replaced under warranty? (Round your answer to three decimal places.)

Answer 1

Answer: 0.034

Explanation:

Given : P(Submitted under warranty)= 0.20

P(Replaced | Submitted under warranty)=0.40

P(Replaced and Submitted under warranty )= P(Submitted under warranty)×P(Replaced | Submitted under warranty)

=
`0.20*0.40=0.08`

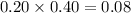
Let x be the number of telephones will end up being replaced under warranty.

Total telephones purchased : n= 10

Using binomial probability formula :
`P(X)=^nC_xp^x(1-p)^(n-x)`

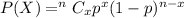
i.e. The probability that exactly three will end up being replaced under warranty will be :-

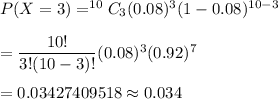`P(X=3)=^(10)C_3(0.08)^3(1-0.08)^(10-3)\\\\=(10!)/(3!(10-3)!)(0.08)^3(0.92)^7\\\\=0.03427409518\approx0.034` [Rounded to three decimal places. ]

Hence, the probability that exactly three will end up being replaced under warranty : 0.034