Question

Kevin Rogers is interested in buying a five-year bond that pays a coupon of 10 percent on a semiannual basis. The current market rate for similar bonds is 8.8 percent. What should be the current price of this bond? (Do not round intermediate computations. Round your final answer to the nearest dollar.)

Answer 1

The bonds price is $1,047.71

Step-by-step explanation:

The present value of a bond will be the coupon payment and maturity discounted at the current market rate.

We assume the bonds face value is 1,000 dollars.

The coupon payment wil be an ordinary annuity:

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C: 1,000 x 10%/2 payment per year = $50

time 10 (5 years x 2 payment per year)

rate 0.044 (8.8% annual / 2 = 4.4% semiannual)

`50 * (1-(1+0.044)^(-10) )/(0.044) = PV\\`

PV $397.5884

Then, maturity will be the present value of a lump sum

`(Maturity)/((1 + rate)^(time) ) = PV`

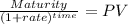
Maturity 1,000.00

time 10.00

rate 0.044

`(1000)/((1 + 0.044)^(10) ) = PV`

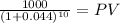
PV 650.12

We add both together and get:

PV of coupon payment + PV of maturity:

$397.5884 + $650.1222 = $1,047.7106