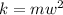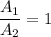Question

Two vertical springs have identical spring constants, but one has a ball of mass m hanging from it and the other has a ball of mass 2m hanging from it. Part A If the energies of the two systems are the same, what is the ratio of the oscillation amplitudes?

Answer 1

`(A_1)/(A_2)=1`

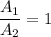
Step-by-step explanation:

given,

two identical spring have identical spring constant

mass 'm' is hanging on one spring and mass of '2m' on another wall.

energy of the two system is same

energy of the system having mass 'm'

`E = (1)/(2)m\omega_1^2A_1^2`

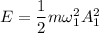
energy of the system having mass '2m'

`E = (1)/(2)(2m)\omega_1^2A_1^2`

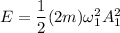
now, Energy are same

`(1)/(2)m\omega_1^2A_1^2= (1)/(2)(2m)\omega_1^2A_1^2`

`(A_1^2)/(A_2^2)=(2\omega_2^2)/(\omega_1^2)`

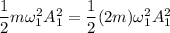
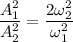
we know
`k = mw^2`

`(A_1)/(A_2)=\sqrt{\frac{2(k)/(m_2)}{{(k)/(m_1)}}`

`(A_1)/(A_2)=\sqrt{(2m_1)/(m_2)}`

`(A_1)/(A_2)=\sqrt{(2m)/(2m)}`

`(A_1)/(A_2)=1`