Question

The legs of a right measure 8 inches and 12 inches. What is the area of the triangle

Answer 1

48

Explanation:

multiply 8 by 12 to get 96, then divide by 2 to get 48

(A=b×h÷2)

Answer 2

The area of the given triangle is 48 inches.

Solution:

Note: Refer the picture attached below

We know that a right triangle always has an angle which is
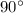`90^(\circ)` and the adjacent sides of the angle is called legs. We can refer the legs also as the base and the height of the triangle (as given in the picture).

Let us assume that the base is b and height is h

As given in the program, b=12, h=8

We know the area of the triangle
`\mathrm{A}=\left((1)/(2)\right) * b * h`

`\mathrm{A}=\left((1)/(2)\right) * 12 * 8`

`=(12)/(2*8)`

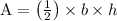
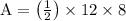
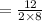
`= (6*8)`= 48

So, the area of the triangle is 48.