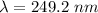Question

The work function of an element is the energy required to remove an electron from the surface of the solid. The work function for rhodium is 480.5 kJ/mol (that is, it takes 480.5 kJ of energy to remove 1 mole of electrons from 1 mole of Rh atoms on the surface of Rh metal). What is the maximum wavelength of light that can remove an electron from an atom in rhodium metal?

Answer 1

`\lambda=249.2\ nm`

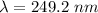
Step-by-step explanation:

Given that:

The work function of the rhodium = 480.5 kJ/mol

It means that

1 mole of electrons can be removed by applying of 480.5 kJ of energy.

Also,

1 mole =
`6.023* 10^(23)\ electrons`

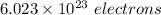
So,

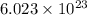`6.023* 10^(23)` electrons can be removed by applying of 480.5 kJ of energy.

1 electron can be removed by applying of
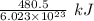`\frac {480.5}{6.023* 10^(23)}\ kJ` of energy.

Energy required =
`79.78* 10^(-23)\ kJ`

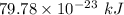
Also,

1 kJ = 1000 J

So,

Energy required =
`79.78* 10^(-20)\ J`

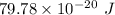
Also,
`E=\frac {h* c}{\lambda}`

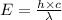
Where,

h is Plank's constant having value
`6.626* 10^(-34)\ Js`

c is the speed of light having value
`3* 10^8\ m/s`

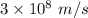
So,

`79.78* 10^(-20)=\frac {6.626* 10^(-34)* 3* 10^8}{\lambda}`

`\lambda=(6.626* 10^(-34)* 3* 10^8)/(79.78* 10^(-20))`

`\lambda=(10^(-26)* \:19.878)/(10^(-20)* \:79.78)`

`\lambda=(19.878)/(10^6* \:79.78)`

`\lambda=2.4916* 10^(-7)\ m`

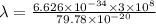
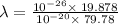
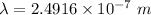
Also,

1 m = 10⁻⁹ nm

So,

`\lambda=249.2\ nm`