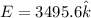Answer:
electric field just above the plate is given as
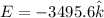
Now electric field just below the plate is given as
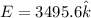
Step-by-step explanation:
Charge density of the plates is given as
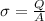
here we know that

Area = (length)(width)
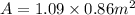
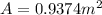
Now we have
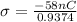
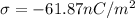
now electric field due to a thin sheet is given by
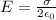
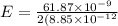

Now electric field just above the plate is given as
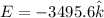
Now electric field just below the plate is given as