Step-by-step explanation:
It is given that, the position of a particle as as function of time t is given by :
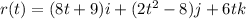
Let v is the velocity of the particle. Velocity of an object is given by :
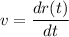
![v=(d[(8t+9)i+(2t^2-8)j+6tk])/(dt)](https://img.qammunity.org/2020/formulas/physics/college/50xv0ctyn8dce6g1gcjvtb2788n283c249.png)
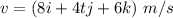
So, the above equation is the velocity vector.
Let a is the acceleration of the particle. Acceleration of an object is given by :
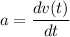
![a=(d[8i+4tj+6k])/(dt)](https://img.qammunity.org/2020/formulas/physics/college/w5wauvkc15jilkrflcp2yso4bdgz0sheeb.png)

At t = 0,
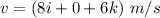

Hence, this is the required solution.