Question

Consider the line segment with end points (0, −6) and (0, −11).

a. What do the ordered pairs of the end points have in common, and what does that mean about the line segment’s location in the coordinate plane?
b. Find the length of the line segment described by finding the distance between its end points (0, −6) and (0, −11).

Answer 1

Answer: See below

Explanation:

a. The ordered pairs (0, -6) and (0, -11) have in common they have the same value on the X-axis.

This means the to point while on diferrent height are one upon the other on the plain, which mean they create a line that is perpendicular to the Y-axis and totaly perpendicular to the X-axis.

b. To calculate the distance between two points on a 2-d space, we can use the following equation:

Distance (D) =
`\sqrt{(x_(1)-x_(2) )^(2) +(y_(1)-y_(2))^(2) }`

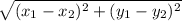
Where the ordered pair
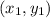`(x_(1), y_(1) )` defines one point and
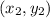`(x_(2), y_(2) )` defines the other.

D =
`\sqrt{(0-0 )^(2) +(-6+11)^(2) }`

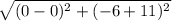
D = 5

The distance between the two points
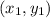`(x_(1), y_(1) )` and
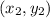`(x_(2), y_(2) )` is 5