Question

Suppose a baby food company has determined that its total revenue R for its food is given by R = − x ^3 + 102 x ^2 + 1575 x where R is measured in dollars and x is the number of units (in thousands) produced. What production level will yield a maximum revenue?

Answer 1

I wish I knew how to do this but I am only on 6th grade lol but I wish I could help you

Answer 2

The production level will yield a maximum revenue when production level is approximately equal to 75,000.

Explanation:

Revenue is given by

R(x) =
`-x^3 + 102x^2 + 1575x`

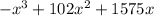
First, we differentiate R(x) with respect to x, to get,

`(d(R(x)))/(dx) = -3x^2 + 204x + 1575`

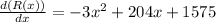
Equating the first derivative to zero, we get,

`(d(R(x)))/(dx) = 0\\\\ -3x^2 + 204x + 1575 = 0`

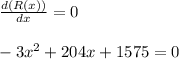
Solving, with the help of quadratic formula, we get,

`x = 75, -7`

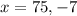
Again differentiation R(x), with respect to x, we get,

`(d^2(R(x)))/(dx^2) = -6x + 204`

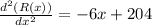
At x = 75

`(d^2(R(x)))/(dx^2) < 0`

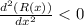
Thus, maxima occurs at x = 75 for R(x).

Thus, the production level will yield a maximum revenue when production level is approximately equal to 75,000.