Question

Suppose that in a senior college class of 500500 ​students, it is found that 215215 ​smoke, 252252 drink alcoholic​ beverages, 215215 eat between​ meals, 124124 smoke and drink alcoholic​ beverages, 7878 eat between meals and drink alcoholic​ beverages, 9191 smoke and eat between​ meals, and 4646 engage in all three of these bad health practices. If a member of this senior class is selected at​ random, find the probability that the student​ (a) smokes but does not drink alcoholic​ beverages; (b) eats between meals and drinks alcoholic beverages but does not​ smoke; (c) neither smokes nor eats between meals.

Answer 1

The probability that the student​ smokes but does not drink alcoholic​ beverages is 0.182.

The probability that the student​ eats between meals and drinks alcoholic beverages but does not​ smoke is 0.064

The probability that the student​ neither smokes nor eats between meals is 0.322

Explanation:

Consider the provided information.

Suppose that in a senior college class of 500 ​students, it is found that 215​smoke, 252 drink alcoholic​ beverages, 215 eat between​ meals, 124 smoke and drink alcoholic​ beverages, 78 eat between meals and drink alcoholic​ beverages, 91 smoke and eat between​ meals, and 46 engage in all three of these bad health practices.

Let A is the represents student smoke.

B is the event, which represents student drink alcoholic beverage.

Part (A) Smokes but does not drink alcoholic​ beverages.

From the above information.

P(A) = 215/500 and P(A ∩ B) = 124/500

Thus,

`P(A\cap B')=P(A)-P(A\cap B)`

`P(A\cap B')=(215)/(500)-(124)/(500)=0.43-0.248=0.182`

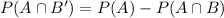
The probability that the student​ smokes but does not drink alcoholic​ beverages is 0.182.

Part (B) Eats between meals and drinks alcoholic beverages but does not​ smoke.

Let C is the event, which represents student eat between meals.

Eats between meals and drinks alcoholic beverages but does not​ smoke can be written as:

`P(C\cap B \cap A')=P(B\cap C)-P(A\cap B \cap C)`

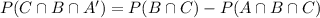
From the given information.

P(B ∩ C) = 78/500 and P(A ∩ B ∩ C)= 46/500

Thus,

`P(C\cap B \cap A')=(78)/(500)-(46)/(500)=0.156-0.092=0.064`

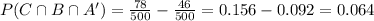
The probability that the student​ eats between meals and drinks alcoholic beverages but does not​ smoke is 0.064

Part (C) Neither smokes nor eats between meals.

Neither smokes nor eats between meals can be written as:

`P((A\cup C)')=1-P(A\cup C)`

From the given information.

P(A) = 215/500 and P(C)= 215/500 and P(A∩C)=91/500

P(A∪C)=P(A)+P(C)-P(A∩C)

P(A∪C)=
`(215)/(500)+(215)/(500)-(91)/(500)=(339)/(500)`

Substitute the respective values in the above formula.

`P((A\cup C)')=1-P(A\cup C)=1-(339)/(500) \\1-0.678=0.322`

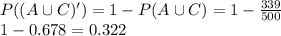
The probability that the student​ neither smokes nor eats between meals is 0.322