Answer:
The points on the curve are
 ,
,
 and
and
 .
.
Explanation:
Step1
For horizontal tangent, derivative of the function and equate to zero.
Given
Equation of curve is given as follows:

Step2
Calculation:
Derivate the function with respect to x and equate to zero as follows:



Now,
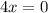
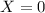
And,

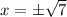
Therefore, the values of
 are
are
 .
.
Step3
Substitute the values of
 in the equation as follows:
in the equation as follows:
For
 ,
,


Therefore, the point is
 .
.
For
 ,
,




Therefore, the point is
 .
.
For
 ,
,




Therefore, the point is
 .
.