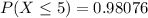Question

This exercise illustrates that poor quality can affect schedulesand costs. A manufacturing process has 100 customer orders tofill. Each order requires one component part that is purchased froma supplier. However, typically, 2% of the components are identifiedas defective, and the components can be assumed to beindependent.a)If the manufacturer stocks 100 components, what is theprobability that the 100 orders can be filled without reorderingcomponents?b) If the manufacturer stocks 102 components, what is theprobability that the 100 orders can be filled without reorderingcomponents?c) If the manufacturer stocks 105 components, what is theprobability that the 100 orders can be filled without reorderingcomponents?

Answer 1

a) 0.13262

b) 0.66575

c) 0.98076

Explanation:

The components manufactured follow a binomial distribution.

In a binomial distribution you have a sequence of independent experiments normally "n" experiments and each experiment in the form of yes or no question with a probability of success "p"

Let X be the variable representing the number of defective components.

The probability of X is calculated as follows for a binomial distribution:

`P( X=n)=(k!)/(n!(k-n)!)p^(n)(1-p)^((k-n))`

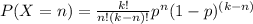
n represents the number of possible defective components

k represents the total number of components

p represents the probability that a component is defective

a)

The probability to fill 100 orders with a stock of 100 components:

n = 0 because you cant have any defective component

k = 100 because thats the available stock

p = 0.02 is the probability of a single component to be defective

`P( X=0)=(100!)/(0!(100-0)!)0.02^(0)(1-0.02)^((100-0))=0.13262`

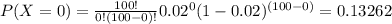
b)

The probability to fill 100 orders with a stock of 102 components:

In this case n can take more than one value, because you have 102 components and only need 100 to be good, meaning you are allowed to have 0, 1 or 2 defective components, so you calculate the probability when n = 0, n = 1 and n = 2 and then add them together, also it can be said as calculating n ≤ 2

`P( X\leq2 )=(102!)/(0!(102-0)!)0.02^(0)(1-0.02)^((102-0))+(102!)/(1!(102-1)!)0.02^(1)(1-0.02)^((102-1))+(102!)/(2!(102-2)!)0.02^(2)(1-0.02)^((102-2))=0.66575`

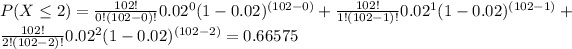
c)

As b, now n can take more values because the stock is 105, calculating for n ≤ 5,

`P(X\leq 5)=0.98076`