Question

Suppose an assembly requires five components from five different vendors. To guarantee starting the assembly on time with 90 percent confidence, what must the service level be for each of the five components? (Assume the same service level for each component).

Answer 1

The service level for each component must be 97.91%

Step-by-step explanation:

If we want a 90% confidence of starting on time, that means we need

`P_{\mbox{starting on time}}=P_{\mbox{every component being ready on time}}=0.9\\`

As the probability of each component being ready is independent from the others, that means that the probability of the 5 components being ready is equal to multiply each probability:

`0.9=P_{\mbox{component 1 ready on time} } * P_{\mbox{component 2 ready on time} } *\\ P_{\mbox{component 3 ready on time} } * P_{\mbox{component 4 ready on time} } *\\P_{\mbox{component 5 ready on time} }`

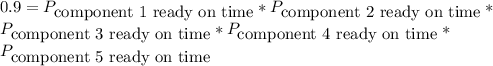
The probability of being ready on time is equal to the service level (in fraction), and all 5 are equal so we can say:

`0.9=(\mbox{service level(in fraction)})^5\\\\\sqrt[5]{0.9} =\mbox{service level(in fraction)}=0.9791\\\mbox{In percentage}: \mbox{service level (in fraction)}*100 = 97.91\%`