Question

Air expands through a turbine from 9 bar, 920 K to 2 bar, 510 K. The inlet velocity is small compared to the exit velocity of 110 m/s. The turbine operates at steady state and develops a power output of 3220 kW. Heat transfer between the turbine and its surroundings and potential energy effects are negligible. Calculate the mass flow rate of air, in kg/s, and the exit area, in m².

Answer 1

m =7.93 kg/s

`A_2=0.054\ m^2`

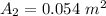
Step-by-step explanation:

Given that

`T_1=920\ K`

`T_2=510\ K`

Inlet velocity is small so

`V_1=0`

`V_2=110\ m/s`

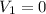
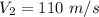
Power develops ,W= 3220 KW

Now from first law of thermodynamics for open system at steady state

`m.h_1+(m.V_1^2)/(2000)+Q=m.h_2+(m.V_2^2)/(2000)+W`

Here given Q=0

m is the mass flow rate in kg/s.

For air

,
`C_p=1.005 KJ/kg.k`

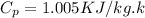
h = m. Cp. T

`m.h_1=m.h_2+(m.V_2^2)/(2000)+W`

`m* 1.005* 920=m* 1.005* 510+(m* 110^2)/(2000)+3220`

`m* (1.005* 920- 1.005* 510-( 110^2)/(2000))=3220`

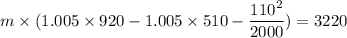
So

m =7.93 kg/s

Mass flow rate of air = 7.93 Kg/s

`m=\rho_2A_2V_2`

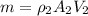
For ideal gas air

`\rho_2=(P_2)/(RT_2)`

`\rho_2=(200)/(0.287* 510)\ kg/m^3`

`\rho_2=1.33\ kg/m^3`

`m=\rho_2A_2V_2`

`7.93=1.33* A_2* 110`

`A_2=0.054\ m^2`

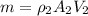
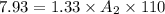
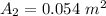
This is the exit area.