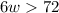For this case we have that by definition, the perimeter of a rectangle is given by:
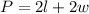
Where:
l: It is the length of the rectangle
w: It is the width of the rectangle
According to the problem data we have:
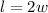
So, the perimeter of the plant is:

If the perimeter must be greater than 72 feet, then we have:
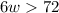
Thus, the inequality that can be used is
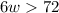
ANswer: