Question

Consider the functions f(x)=4x+15 and g(x)=x^2-x+6. At what positive integer value of x does the quadratic function, g(x), begin to exceed the linear function, f(x)?

Answer 1

At the positive integer value of x=7 the quadratic function begin to exceed the linear function

Explanation:

we have

`f(x)=4x+15`

`g(x)=x^(2)-x+6`

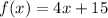
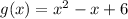
using a graphing tool

see the attached figure

For x < -1.405 and x > 6.405 the quadratic function begin to exceed the linear function

so

At the positive integer value of x=7 the quadratic function begin to exceed the linear function