Answer:
(a)
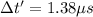
(b)

Step-by-step explanation:
We use Lorentz transformations, since they relate the measures of a physical magnitude obtained by two different observers, these are:

Here
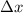 is the spatial separation according to O,
is the spatial separation according to O,
 is the spatial separation according to O',
is the spatial separation according to O',
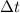 is the time interval according to O,
is the time interval according to O,
 is the time interval according to O',
is the time interval according to O',
 is the relative speed between the two observers and
is the relative speed between the two observers and
 is the speed of light. All we do now is write the quantities we were given, recall that
is the speed of light. All we do now is write the quantities we were given, recall that
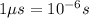
(a)
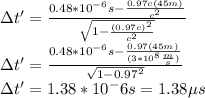
(b)
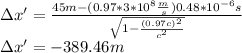
The minus sign means that the second event is closer for one observer and the first is closer for the other.