Question

Calculate the total mass of water in kg on Earth's surface from the following data: total planetary surface area: 510,066,000 km2, land area of planet: 148,647,000 km2 , assume the average depth of water is:100.0km and the density of water is 1.00g/mL

(using dimensional analysis)

Answer 1

The total mass of water in on Earth's surface is
`3.61419* 10^(22) kg`.

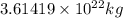Step-by-step explanation:

Total planetary surface area = T =
`510,066,000 km^2`

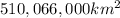
Total land area of planet = L =
`148,647,000 km^2`

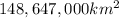
Total water area of planet = W

T = L + W

`510,066,000 km^2=148,647,000 km^2-W`

`W=510,066,000 km^2-148,647,000 km^2=361,419,000 km^2`

Volume = Area × Depth

Volume of water on earth = V

V=
`361,419,000 km^2* 100 km^=36,141,900,000 km^3`

`km^3=10^(12) L`

`V=36,141,900,000 km^3=36,141,900,000 * 10^(12) L`

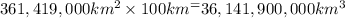
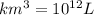
Total mass of total water on the earth = M

Density of the water,D = 1 g/mL = 0.001 kg/0.001 L=1 kg/L

1 g - 0.001 kg

1 mL = 0.001 L

`D=(M)/(V)`

`M=D* V`

`M =1 kg/L* 36,141,900,000 * 10^(12) L=3.61419* 10^(22) kg`

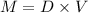
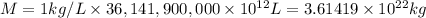
The total mass of water in on Earth's surface is
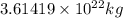`3.61419* 10^(22) kg`.