Question

In a certain region, suppose the ages of smartphone users approximately follow a normal distribution with approximate mean and standard deviation of 39.9 years and 9.1 years, respectively. Determine the probability that a random smartphone user is at most 48 years old. • Round your answer to four decimal places.

Answer 1

0.8133.

Explanation:

We have been given that the ages of smartphone users approximately follow a normal distribution with approximate mean and standard deviation of 39.9 years and 9.1 years, respectively.

First of all, we will use z-score formula to find z-score of 48.

`z=(x-\mu)/(\sigma)`, where,

`z` = z-score,

`x` = Sample score,

`\mu` = Mean,

`\sigma` = Standard deviation.

Substitute the given values:

`z=(48-39.9)/(9.1)`

`z=(8.1)/(9.1)`

`z=0.89`

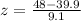
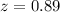
Now, we will need to find the probability of z-score less than or equal to 0.89 as:

`P(z\leq 0.89)`

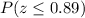
Using normal distribution table, we will get:

`P(z\leq 0.89)=0.81327`

`P(z\leq 0.89)\approx 0.8133`

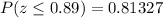
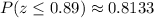
Therefore, the probability that a random smartphone user is at most 48 years old would be 0.8133.